Towards Reliable Empirical Machine Unlearning Evaluation: A Game-Theoretic View

arXiv

Brief Summary

Despite the fast-paced development of the machine unlearning community, the evaluation of the performance of machine unlearning algorithms remains a big open problem due to the lack of a unified framework and rigorous justification. In this work, we theoretically formalized the unlearning sample inference game for provable and reliable empirical evaluation of machine unlearning algorithms, tackling one of the most foundational problems in this field.

Unlearning Sample Inference Game

The idea is simple: we split the data into three parts called retain set, forget set, and test set, and request the defender to learn on the retain set plus the forget set, and then unlearn the forget set at the end. On the other hand, we throw a bunch of data to the adversary from either only the forget set or the test set, and let the adversary guess which set we're using. Intuitively, if the forget set's information is left in the unlearned model, then the adversary can just feed the data we throw to it to the unlearned model, and infer something non-trivial.

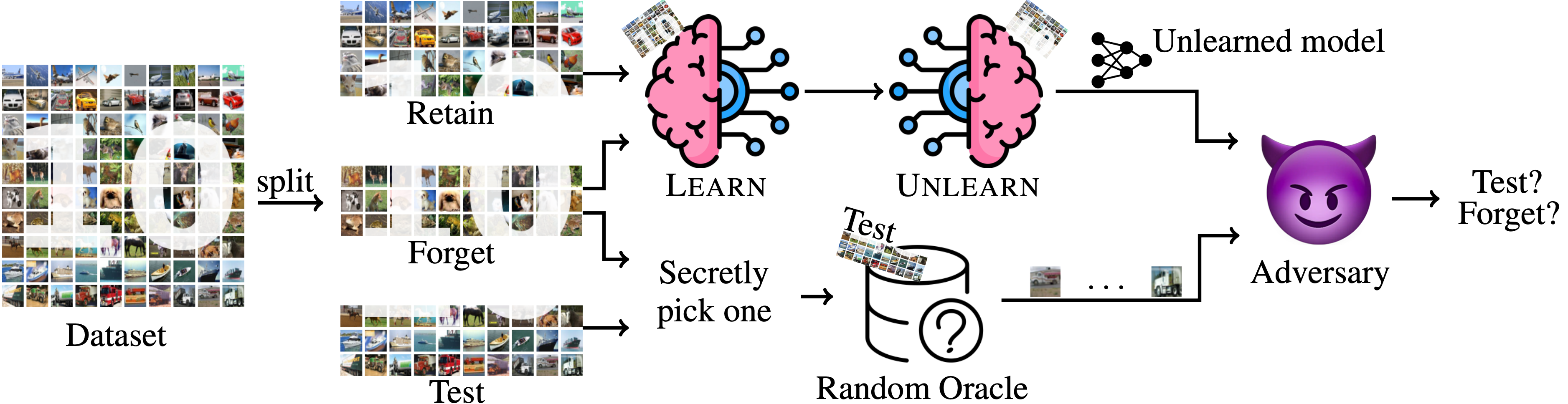
It turns out that using the idea of advantage, we can formalize a natural metric called Unlearning Quality $\mathcal{Q}$ that measures the quality of the unlearning algorithm. We then prove that

1. For the gold-standard unlearning method, i.e., the retraining method, we always have $\mathcal{Q} = 1$.
2. For some $(\epsilon , \delta )$-certified removal method,¹ we always have $\mathcal{Q} \geq \frac{4 - 4 \delta }{e^{\epsilon } + 1} - 1$.

To our knowledge, this is the first unlearning performance metric that achieves such formal guarantees.

Practical Evaluation

In practice, $\mathcal{Q}$ is impossible to evaluate due to the complexity. Hence, we further propose an efficient approximation algorithm to compute $\mathcal{Q}$, and demonstrate the efficacy on real-life datasets.

Citation

@article{tu2024towards,
  title   = {Towards Reliable Empirical Machine Unlearning Evaluation: A Game-Theoretic View},
  author  = {Tu, Yiwen and Hu, Pingbang and Ma, Jiaqi},
  journal = {arXiv preprint arXiv:2404.11577},
  year    = {2024}
}